1MARK QUESTIONS
- What is blackbody radiation?
Blackbody radiation is the electromagnetic radiation emitted by an idealized perfect absorber (blackbody) at a given temperature. It depends only on the temperature and follows Planck's law, covering all wavelengths.
- An iron rod is heated. The colors at different temperatures are noted. Which of the colors (Orange, Red, White, Blue) shows that the iron rod is at the lowest temperature?
Red shows the lowest temperature. As temperature increases, the color shifts from red (lower energy, longer wavelength) to orange, white, and finally blue (higher energy, shorter wavelength) due to Wien's displacement law.
- What are the different hypotheses of a blackbody radiation?
- Rayleigh-Jeans hypothesis: Assumes continuous energy distribution, leading to the ultraviolet catastrophe.
- Planck's hypothesis: Energy is emitted in discrete quanta (\( E = h\nu \)), resolving the blackbody spectrum.
- Wien's displacement law: Peak wavelength shifts with temperature. - Define stopping potential and work function?
- Stopping Potential: The minimum reverse voltage needed to stop photoelectrons emitted in the photoelectric effect.
- Work Function: The minimum energy required to eject an electron from a material's surface. - Is stopping potential dependent on intensity or frequency? Justify your answer.
Stopping potential depends on frequency, not intensity. It is determined by the energy of incident photons (\( E = h\nu \)) exceeding the work function, as per Einstein's photoelectric equation (\( eV_s = h\nu - \phi \)). Intensity affects photocurrent but not the stopping voltage.
- Is photocurrent dependent on intensity or frequency? Justify your answer.
Photocurrent depends on intensity, not frequency. Intensity determines the number of photons, which affects the number of ejected electrons, thus the current. Frequency must exceed the threshold for emission but doesn’t scale the current.
- State de-Broglie hypothesis.
De-Broglie hypothesized that all matter exhibits wave-like behavior, with an associated wavelength given by \( \lambda = \frac{h}{p} \), where \( h \) is Planck's constant and \( p \) is the momentum.
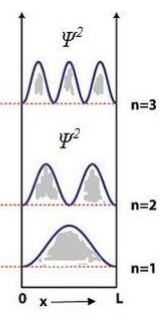
- Draw the probability of the particle for energy levels (n = 1, 2, 3) in one-dimensional potential box.
The probability density \( |\psi_n(x)|^2 \) for a particle in a 1D box (0 to L) is sinusoidal: for \( n = 1 \), one peak; \( n = 2 \), two peaks; \( n = 3 \), three peaks, with nodes increasing with \( n \).
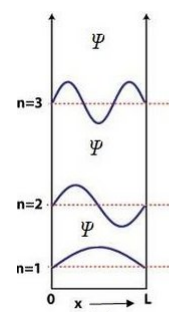
- Draw the wave function of the particle for energy levels (n = 1, 2, 3) in one-dimensional potential box.
The wave function \( \psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right) \) has: \( n = 1 \), one half-sine wave; \( n = 2 \), one full sine wave; \( n = 3 \), one and a half waves, with nodes at boundaries and within the box.
- Explain Heisenberg's Uncertainty Principle.
Heisenberg's Uncertainty Principle states that it is impossible to simultaneously know the exact position (\( x \)) and momentum (\( p \)) of a particle with perfect precision, mathematically \( \Delta x \cdot \Delta p \geq \frac{\hbar}{2} \), where \( \hbar \) is the reduced Planck's constant. This arises from the wave-particle duality.
- Write any two laws of photoelectric effect.
- The kinetic energy of photoelectrons is proportional to the frequency of incident light (\( K_{\text{max}} = h\nu - \phi \)). - No photoelectrons are emitted if the frequency is below a threshold value (dependent on the work function).
- Prove that bodies at rest are not associated with matter waves.
According to de-Broglie, \( \lambda = \frac{h}{p} \), where \( p = mv \). For a body at rest (\( v = 0 \)), momentum \( p = 0 \), making \( \lambda \) infinite or undefined. Thus, matter waves are not associated with stationary bodies.
- Show that matter waves travel faster than light.
We start with the equation
\[ h\nu = mc^2 \]
\[ \nu = \frac{mc^2}{h} \]
Matter wave velocity can be written as,
\[ w = \nu \lambda \]
Let's substitute values of \( \lambda \) and \( \nu \), we get
\[ w = \frac{mc^2}{h} \times \frac{h}{mv} \]
\[ w = \frac{c^2}{v} \]
Velocity of the particle can’t exceed the speed of light, \( w > c \).
- What is wavefunction? Write any two of its properties.
- Wavefunction (\( \psi \)): A mathematical function describing the quantum state of a particle, with \( |\psi|^2 \) giving the probability density.
- Properties:
1. It must be continuous and single-valued.
2. It is normalized (\( \int |\psi|^2 \, dx = 1 \)). - What is the outcome of G.P. Thomson experiment?
G.P. Thomson's experiment demonstrated electron diffraction through a thin metal foil, confirming the wave nature of electrons and supporting de-Broglie's hypothesis, analogous to X-ray diffraction.
- Distinguish classical and quantum gates.
- Classical Gates: Operate on bits (0 or 1) using Boolean logic (e.g., AND, OR, NOT), deterministic and reversible only with additional steps.
- Quantum Gates: Operate on qubits (superpositions of 0 and 1), use unitary transformations (e.g., Hadamard, CNOT), and are inherently reversible. - Enumerate the phenomena from quantum mechanics that are used in quantum computing.
- Superposition.
- Entanglement.
- Interference. - In quantum computing, what is the basic unit of information?
The basic unit of information is a qubit (quantum bit), which can exist in a superposition of 0 and 1 states.
- What distinguishes a quantum computer from a classical one?
Quantum computers use qubits with superposition and entanglement, enabling parallel computation, whereas classical computers use bits with sequential processing.
- Explain quantum cryptography in simple words.
Quantum cryptography uses quantum mechanics (e.g., photon polarization) to securely share encryption keys. Any eavesdropping disturbs the quantum state, alerting users, making it highly secure.
- Will quantum computing replace classical computing?
No, quantum computing is unlikely to fully replace classical computing. It will complement it for specific tasks (e.g., cryptography, optimization), while classical computers handle general-purpose tasks efficiently.
- Which company has a quantum computer that we can use through their website?
IBM offers access to its quantum computers (e.g., IBM Quantum Experience) via their website.
- In a quantum circuit, a memory consisting of n bits of information has ___ possible states.
\( 2^n \) possible states (due to superposition of all combinations of 0 and 1).
- Write any two applications of quantum computers.
- Cryptography (breaking or creating secure codes).
- Drug discovery (simulating molecular interactions). - What are some open questions about quantum computing?
- Scalability of quantum hardware.
- Error correction in quantum systems.
- Practical advantages over classical computing for all problems.