Kronig–Penney Model – Theory, Derivation & Band Structure
Bloch's Theorem
Bloch’s theorem describes the nature of wave functions for quantum mechanical particle ( like electron) in a periodic potential.
\[ \psi(r) = e^{ik.r}U(r)\] where r is position, \(\psi\) is the wave function, \(U\) is a periodic function with the same periodicity as the crystal, the wave vector \(k\) is the crystal momentum vector, \(e\) is Euler's number, and \(i\) is the imaginary unit.Quick Exam Notes
- Concept: The Kronig–Penney model explains how periodic potentials in a crystal lattice lead to the formation of energy bands and band gaps.
- Key Equation (Dispersion Relation): \( \frac{Psin\alpha a}{\alpha a}+cos(\alpha a) = \cos(ka) \), derived using Schrödinger’s equation + Bloch’s theorem.
- Allowed & Forbidden Bands: Real solutions for \( k \) → allowed energy bands; no solutions → forbidden gaps (band gaps).
- Special Limits:
- Barrier height \( \rightarrow \) 0 ⇒ Free electron model.
- Barrier height \( \rightarrow \infty \) ⇒ Tight-binding model (narrow allowed bands).
- Applications: Explains band theory of solids \( \rightarrow \) conductors, semiconductors, and insulators.
- Scroll to the end of the page to explore the Interactive Visualization demo of Kronig-Penny Model.
Kronig-Penny Model
The Kronig–Penney model is a simple way to understand how electrons move inside a crystal (solid). In a crystal, the atoms (ions) are arranged in a regular repeating pattern, and this creates a periodic potential for the electrons. According to this model:
- Near the positive ions, the potential energy of the electron is almost zero (very small).
- Between two ions (midway), the potential energy becomes the highest.
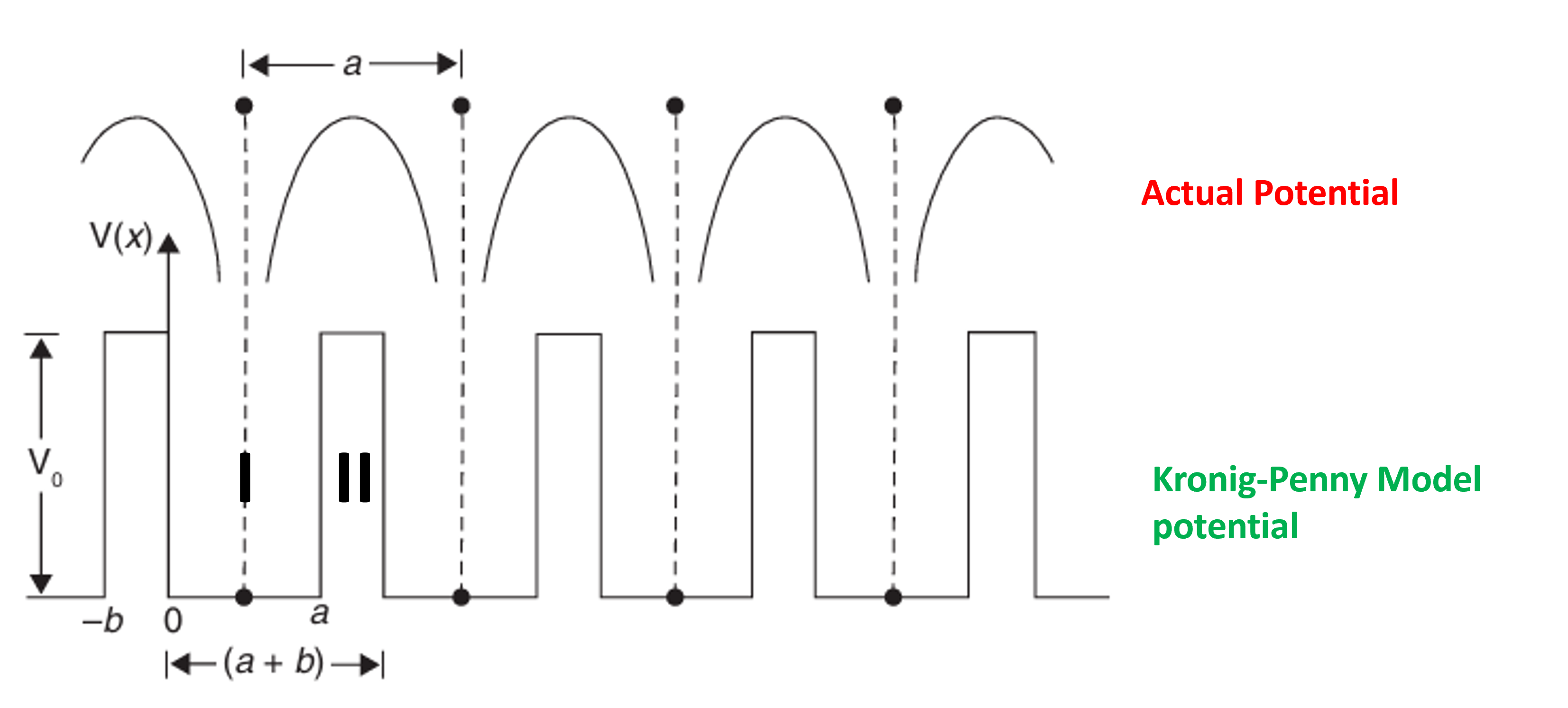
Figure 1: Kronig–Penney model diagram illustrating periodic potential wells and barriers in a crystal lattice.
The potential energy for region-I and region-II can be written as, \[ V(x) = \begin{cases} 0, & 0 \leq x \leq a \\ V_0, & -b< x < a \end{cases} \quad \tag{1} \] The time independent Schrodinger equation for a particle in one dimensional box is given by \[ \frac{d^2 \psi}{dx^2} + \frac{2m(E - V)}{\hbar^2} \psi = 0 \] Region-\(\mathrm{I}\): \[ \frac{d^2 \psi}{dx^2} + \alpha^2 \psi = 0 \quad ; \quad \alpha^2 = \frac{2mE}{\hbar^2} \tag{2}\] Region-\(\mathrm{II}\): \[ \frac{d^2 \psi}{dx^2} + \beta^2 \psi = 0; \quad \beta^2 = \frac{2m(E-V_0)}{\hbar^2} \tag{3}\] The solution of this equation have the form (According to Bloch's theorem) \[ \psi(x) = U_k(x) e^{ikx} \] Where \(U_k(x)\) is periodic with periodicity of the lattice, That is \[U_k(x+a) = U_k(a) \] The form \(U_k\) depends on the exact nature of potential field. The solutions for the Eqn(2) are possible only for energies given by the relation: \[ \boxed{\frac{Psin\alpha a}{\alpha a}+cos \alpha a = cos ka }\tag{4} \] Where P is scattering power of the potantial barrier, \[ P = \frac{4\pi^2ma}{h^2}V_0 w \] The equation (4) tells us that the right-hand side of the function can only take values between +1 and −1. This means that not all values of α are possible—only certain values are allowed. As a result, the energy E of an electron cannot take any random value; instead, it is restricted to specific ranges. These ranges of allowed energy values are what we call energy bands (or zones).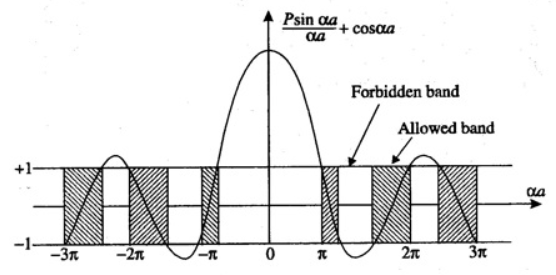
Figure 2: Equation and potential well representation used in the derivation of the Kronig–Penney model.
Observations
- When \( P \rightarrow 0 \) \[ cos \alpha a = cos ka\] Thus \(k = \alpha \), \[ k^2 = \alpha^2 = \frac{2mE}{\hbar^2} \] \[ E = \frac{\hbar^2k^2}{2m} \] \[ E = \frac{4h^2\pi^2}{8m\lambda^2\pi^2} ( \because k = \frac{2\pi}{\lambda} \& \hbar = \frac{h}{2\pi}) \] \[ E = \frac{h^2}{2m\lambda^2} \] \[ E = \frac{h^2p^2}{2mh^2} ( \because \lambda = \frac{h}{p})\] \[ E = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m} = \frac{1}{2}mv^2 \] This indicates that the total energy of the electron comes only from kinetic energy and the electron can move freely inside the crystal without being restricted by potential energy. In such a case, the material behaves like a conductor, because free electrons are available to carry electric current.
- When \( P \rightarrow \infty \); Similarly, we get \[E = \frac{n^2h^2}{8ma^2} \] This indicates that the energy values are discrete (fixed, not continuous). This means the electron is trapped inside the potential well and cannot move freely. Therefore, this situation represents an insulator, where no free electrons are available for conduction.
The Kronig–Penney model explains the motion of electrons in a periodic potential of a crystal lattice. It shows that allowed and forbidden energy bands are formed. This model helps in classifying solids as conductors, semiconductors, or insulators based on their band structure.
E vs k diagram
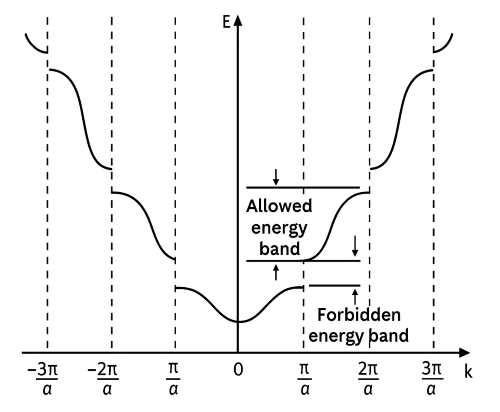
Figure 3: E vs k band structure from the Kronig–Penney model, showing allowed energy bands and forbidden gaps.
The 𝐸 vs 𝑘 diagram shows how the energy (𝐸) of electrons in a solid varies with their wave vector (𝑘). In a crystal, electrons do not have continuous energy values but instead form allowed energy bands separated by forbidden gaps called band gaps. At certain values of 𝑘, the energy levels split due to the periodic potential of the lattice. The lowest band is the valence band, filled with electrons, while the next higher band is the conduction band, which is usually empty. The band gap is the energy difference between the top of the valence band and the bottom of the conduction band. This diagram helps us understand whether a material behaves as a conductor, semiconductor, or insulator: conductors have overlapping bands, semiconductors have a small band gap, and insulators have a large band gap. Thus, the 𝐸 vs 𝑘 diagram is a powerful tool to visualize the electronic structure of materials.Applications of Kronig Penny Model
- It explains the origin of allowed and forbidden energy bands in solids.
- It helps in classifying materials into conductors, semiconductors, and insulators.
- It improves the free electron theory by including the effect of periodic potential of ions.
- It provides the foundation for band theory, which is essential to study solid-state devices.
- It helps in understanding the electrical, optical, and thermal properties of solids.
Interactive visualisation of Kronig-Penny Model
Interactive Visualisation of Allowed and Forbidden bands
Use the interactive visualization below to explore how different parameters affect the band structure in the Kronig-Penney model. Adjust the potential strength and barrier width to see how energy bands and band gaps change.
Band Structure Visualization
Summary
The Kronig–Penney model is a one-dimensional quantum mechanical model used to explain the formation of allowed and forbidden energy bands in solids. By solving the Schrödinger equation for electrons in a periodic potential of alternating barriers and wells, and applying Bloch’s theorem, a dispersion relation is derived that distinguishes between allowed bands (real solutions) and band gaps (no solutions). In limiting cases, the model reduces to the free-electron approximation or the tight-binding approximation. This simple but powerful model forms the foundation of band theory in solid state physics and is essential for understanding conductors, insulators, and semiconductors.
MCQs on Kronig–Penney Model
-
The Kronig–Penney model is used to explain:
- a) Nuclear binding energy
- b) Band structure in solids
- c) Superconductivity
- d) Radioactive decay
Answer
b) Band structure in solids
-
The potential assumed in the Kronig–Penney model is:
- a) Constant potential
- b) Periodic potential of wells and barriers
- c) Coulomb potential
- d) Delta function potential only
Answer
b) Periodic potential of wells and barriers
-
The dispersion relation in the Kronig–Penney model determines:
- a) Only forbidden gaps
- b) Allowed energy bands and forbidden gaps
- c) Magnetic susceptibility
- d) Crystal lattice constant
Answer
b) Allowed energy bands and forbidden gaps
-
In the limiting case where the barrier height tends to zero, the Kronig–Penney model reduces to:
- a) Tight-binding model
- b) Free electron model
- c) Hydrogen atom model
- d) Drude model
Answer
b) Free electron model
-
Which concept is fundamental in deriving the Kronig–Penney model?
- a) Heisenberg uncertainty principle
- b) Bloch’s theorem
- c) Pauli exclusion principle
- d) Einstein’s photoelectric equation
Answer
b) Bloch’s theorem